安全側の考えとは
1.落石シミュレーション
落石対策に関する調査設計業務を受注した。発注者との初回打合せに向けて、社内で事前協議をしていたときの話である。
主担当のO主任より、「落石の運動エネルギーの予測にシミュレーション解析を使用する」という説明があった。我が社で使用している落石シミュレーションソフトは、「右城らの手法」である。
『なぜ「右城らの手法」を採用することにしたのか』と質問すると、『よく使われている「○○らの手法」と比較した結果、「右城らの手法」が落石の速度が速くなる傾向があり、安全側であるので
決めた』という回答であった。
技術者の答弁になっていない。「実験結果や斜面上の痕跡を上手く再現できる」とか、「使用しているアルゴリズムが力学的に合理的である」といった説明をしてくれれば嬉しいのであるが、自分の意見をきちっと述べられる技術者は少ない。「この技術基準に基づいている」「安全側である」と答える技術者が多い。情けない限りである。
2.斜面安定解析
平成11年(1999年)に、「土木構造物設計・施工の盲点」という本を理工図書から出版した。実務者がよく勘違いしている事例や、技術基準書の誤りを指摘したものである。
斜面安定解析にまつわる話の中で、「グラウンドアンカーを設置した場合の安定解析式が、一つの技術基準書であるにも関わらず2種類ある。地すべり対策では式(1)が、切土のり面対策では式(2)が使われている。力学的に合理的なのは式(2)である。この式に統一すべきである」とう趣旨の指摘をしたのであるが、未だ改善されていない。
Fs={∑(cl+Wcosαtanφ)+P(cosθ+sinθtanφ)}/∑Wsinα ・・・・式(1)
Fs={∑(cl+Wcosαtanφ)+Psinθtanφ}/(∑Wsinα-Pcosθ) ・・・・式(2)
つい最近の「地すべり学会誌」Vol.49,No.3,2012に、榎田充哉氏が「斜面防災分野の学術論文に蔓延する不思議な数学」という論説を発表していた。その中の1つに、「強さと力の足し算」の話があり、地すべり対策における安定解析について驚くべきことが紹介されている。
『昭和50年代に地すべり抑止工は「地すべりの抵抗力を増加させる工法」か「地すべりの活動力を低下させる工法」か、という議論が実務者や研究者の中でなされた。前者の"抵抗力を増加させる工法"という概念論はそれ以前から採用されており、安定解析式の分子項に抑止工効果を加算する方法がその当時すでに主流になっていた。後者を提案していた実務者や研究者は数学的(力学的)に正しい方法として後者を提案したが、概念論を優先する勢力が数学を無視する形となった。前者の場合、アンカー工などの抑止工の抑止力は安定安定解析の分子項に加算され「強さ+力=強さ」という不思議な数学が採用されている。現在の斜面防災関係の技術基準書で前者の式を掲載している基準書と後者の式を掲載している基準書が存在するのはそれぞれの流れを受けたものである』
さらに驚くべきことが紹介されている。
『平成9年に改訂された、この分野で最も著名な技術基準書の改訂に関する説明書には"抑止工の効果は力学的には分母から引く方法が正しいが、安全側をみて分子に加算する方法を採用した"という趣旨の説明がなされていた』
「理論が間違っていても、安全率が小さく与えられれば許される」という論理がまかり通ることに正直驚かされると同時に、正しい論理が受け入れられない組織があることの恐ろしさを感じた。
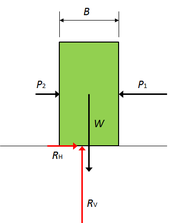
3. 床に置かれたブロックの安定問題
斜面安定解析の問題が理解できない方も少なくないと思う。そこで、床に置かれたブロックの安定問題として説明することにする。このように考えれば容易に理解できることと思う。
右図に示すように、平坦な床に幅Bのブロックが置かれている。ブロックの自重をW、ブロックと床の摩擦角はφ、付着強度はcとする。ブロックの右側をP1の力で押し、ブロックの左側からは逆向きにP2の力で押す場合について、滑動の安全率を考えて見よう。
【解答A】
床からの鉛直反力(∑V=0より) RV=W
床からの水平反力(∑H=0より) RH=P1-P2
ブロック底面と床面の抵抗力 Ru=RVtanφ+cB=Wtanφ+cB
滑動の安全率 Fs=Ru/RH=(Wtanφ+cB)/(P1-P2) ・・・・・式(3)
Fs>=1.0ならブロックは静止していることになる。
Fs<1.0ならブロックは左側にすべり運動をすることになる。
【解答B】
ブロックを左側に滑らそうとする力 P1
滑動に対する抵抗力 Wtanφ+cB+P2
滑動の安全率 Fs=(Wtanφ+cB-P2)/P1 ・・・・・・・・・式(4)
(Wtanφ+cB)は、ブロックが水平力に耐えることができる抵抗力であり、作用力ではない。底面に作用する力はRHである。RHの最大が(Wtanφ+cB)となるのである。
解答A が正しくて、解答Bが間違っていることは、容易に理解されよう。式(1)は式(4) に、式(2)は式(3)に相当する。
 日々進化
日々進化

